Coding the Solution

Time to code the final solution!

Finish the code in the function search, which will create a tree of possibilities and traverse it using DFS until it finds a solution for the sudoku puzzle.

Start Quiz:

function.py utils.py solution.py

from utils import *

def search(values):
    "Using depth-first search and propagation, create a search tree and solve the sudoku."
    # First, reduce the puzzle using the previous function
    
    # Choose one of the unfilled squares with the fewest possibilities
    
    # Now use recursion to solve each one of the resulting sudokus, and if one returns a value (not False), return that answer!

    # If you're stuck, see the solution.py tab!

rows = 'ABCDEFGHI'
cols = '123456789'

def cross(a, b):
    return [s+t for s in a for t in b]

boxes = cross(rows, cols)

row_units = [cross(r, cols) for r in rows]
column_units = [cross(rows, c) for c in cols]
square_units = [cross(rs, cs) for rs in ('ABC','DEF','GHI') for cs in ('123','456','789')]
unitlist = row_units + column_units + square_units
units = dict((s, [u for u in unitlist if s in u]) for s in boxes)
peers = dict((s, set(sum(units[s],[]))-set([s])) for s in boxes)

def display(values):
    """
    Display the values as a 2-D grid.
    Input: The sudoku in dictionary form
    Output: None
    """
    width = 1+max(len(values[s]) for s in boxes)
    line = '+'.join(['-'*(width*3)]*3)
    for r in rows:
        print(''.join(values[r+c].center(width)+('|' if c in '36' else '')
                      for c in cols))
        if r in 'CF': print(line)
    return

def grid_values(grid):
    """
    Convert grid into a dict of {square: char} with '123456789' for empties.
    Input: A grid in string form.
    Output: A grid in dictionary form
            Keys: The boxes, e.g., 'A1'
            Values: The value in each box, e.g., '8'. If the box has no value, then the value will be '123456789'.
    """
    chars = []
    digits = '123456789'
    for c in grid:
        if c in digits:
            chars.append(c)
        if c == '.':
            chars.append(digits)
    assert len(chars) == 81
    return dict(zip(boxes, chars))
    
def eliminate(values):
    """
    Go through all the boxes, and whenever there is a box with a value, eliminate this value from the values of all its peers.
    Input: A sudoku in dictionary form.
    Output: The resulting sudoku in dictionary form.
    """
    solved_values = [box for box in values.keys() if len(values[box]) == 1]
    for box in solved_values:
        digit = values[box]
        for peer in peers[box]:
            values[peer] = values[peer].replace(digit,'')
    return values

def only_choice(values):
    """
    Go through all the units, and whenever there is a unit with a value that only fits in one box, assign the value to this box.
    Input: A sudoku in dictionary form.
    Output: The resulting sudoku in dictionary form.
    """
    for unit in unitlist:
        for digit in '123456789':
            dplaces = [box for box in unit if digit in values[box]]
            if len(dplaces) == 1:
                values[dplaces[0]] = digit
    return values

def reduce_puzzle(values):
    """
    Iterate eliminate() and only_choice(). If at some point, there is a box with no available values, return False.
    If the sudoku is solved, return the sudoku.
    If after an iteration of both functions, the sudoku remains the same, return the sudoku.
    Input: A sudoku in dictionary form.
    Output: The resulting sudoku in dictionary form.
    """
    solved_values = [box for box in values.keys() if len(values[box]) == 1]
    stalled = False
    while not stalled:
        solved_values_before = len([box for box in values.keys() if len(values[box]) == 1])
        values = eliminate(values)
        values = only_choice(values)
        solved_values_after = len([box for box in values.keys() if len(values[box]) == 1])
        stalled = solved_values_before == solved_values_after
        if len([box for box in values.keys() if len(values[box]) == 0]):
            return False
    return values

from utils import *

def search(values):
    "Using depth-first search and propagation, try all possible values."
    # First, reduce the puzzle using the previous function
    values = reduce_puzzle(values)
    if values is False:
        return False ## Failed earlier
    if all(len(values[s]) == 1 for s in boxes): 
        return values ## Solved!
    # Choose one of the unfilled squares with the fewest possibilities
    n,s = min((len(values[s]), s) for s in boxes if len(values[s]) > 1)
    # Now use recurrence to solve each one of the resulting sudokus, and 
    for value in values[s]:
        new_sudoku = values.copy()
        new_sudoku[s] = value
        attempt = search(new_sudoku)
        if attempt:
            return attempt

User's Answer:

(Note: The answer done by the user is not guaranteed to be correct)

function.py utils.py solution.py

from utils import *

def search(values):
    "Using depth-first search and propagation, create a search tree and solve the sudoku."
    # First, reduce the puzzle using the previous function
    values = reduce_puzzle(values)
    if values is False:
        return False ## Failed earlier
    if all(len(values[s]) == 1 for s in boxes): 
        return values
        
    # If you're stuck, see the solution.py tab!
    minvalue = 10
    for box in boxes:
        if len(values[box]) > 1:
            if len(values[box]) < minvalue:
                minvalue = len(values[box])
                bestbox = box
    for value in values[bestbox]:
        new_sudoku = values.copy()
        new_sudoku[bestbox] = value
        attempt = search(new_sudoku)
        if attempt:
            return attempt

rows = 'ABCDEFGHI'
cols = '123456789'

def cross(a, b):
    return [s+t for s in a for t in b]

boxes = cross(rows, cols)

row_units = [cross(r, cols) for r in rows]
column_units = [cross(rows, c) for c in cols]
square_units = [cross(rs, cs) for rs in ('ABC','DEF','GHI') for cs in ('123','456','789')]
unitlist = row_units + column_units + square_units
units = dict((s, [u for u in unitlist if s in u]) for s in boxes)
peers = dict((s, set(sum(units[s],[]))-set([s])) for s in boxes)

def display(values):
    """
    Display the values as a 2-D grid.
    Input: The sudoku in dictionary form
    Output: None
    """
    width = 1+max(len(values[s]) for s in boxes)
    line = '+'.join(['-'*(width*3)]*3)
    for r in rows:
        print(''.join(values[r+c].center(width)+('|' if c in '36' else '')
                      for c in cols))
        if r in 'CF': print(line)
    return

def grid_values(grid):
    """
    Convert grid into a dict of {square: char} with '123456789' for empties.
    Input: A grid in string form.
    Output: A grid in dictionary form
            Keys: The boxes, e.g., 'A1'
            Values: The value in each box, e.g., '8'. If the box has no value, then the value will be '123456789'.
    """
    chars = []
    digits = '123456789'
    for c in grid:
        if c in digits:
            chars.append(c)
        if c == '.':
            chars.append(digits)
    assert len(chars) == 81
    return dict(zip(boxes, chars))
    
def eliminate(values):
    """
    Go through all the boxes, and whenever there is a box with a value, eliminate this value from the values of all its peers.
    Input: A sudoku in dictionary form.
    Output: The resulting sudoku in dictionary form.
    """
    solved_values = [box for box in values.keys() if len(values[box]) == 1]
    for box in solved_values:
        digit = values[box]
        for peer in peers[box]:
            values[peer] = values[peer].replace(digit,'')
    return values

def only_choice(values):
    """
    Go through all the units, and whenever there is a unit with a value that only fits in one box, assign the value to this box.
    Input: A sudoku in dictionary form.
    Output: The resulting sudoku in dictionary form.
    """
    for unit in unitlist:
        for digit in '123456789':
            dplaces = [box for box in unit if digit in values[box]]
            if len(dplaces) == 1:
                values[dplaces[0]] = digit
    return values

def reduce_puzzle(values):
    """
    Iterate eliminate() and only_choice(). If at some point, there is a box with no available values, return False.
    If the sudoku is solved, return the sudoku.
    If after an iteration of both functions, the sudoku remains the same, return the sudoku.
    Input: A sudoku in dictionary form.
    Output: The resulting sudoku in dictionary form.
    """
    solved_values = [box for box in values.keys() if len(values[box]) == 1]
    stalled = False
    while not stalled:
        solved_values_before = len([box for box in values.keys() if len(values[box]) == 1])
        values = eliminate(values)
        values = only_choice(values)
        solved_values_after = len([box for box in values.keys() if len(values[box]) == 1])
        stalled = solved_values_before == solved_values_after
        if len([box for box in values.keys() if len(values[box]) == 0]):
            return False
    return values

from utils import *

def search(values):
    "Using depth-first search and propagation, try all possible values."
    # First, reduce the puzzle using the previous function
    values = reduce_puzzle(values)
    if values is False:
        return False ## Failed earlier
    if all(len(values[s]) == 1 for s in boxes): 
        return values ## Solved!
    # Choose one of the unfilled squares with the fewest possibilities
    n,s = min((len(values[s]), s) for s in boxes if len(values[s]) > 1)
    # Now use recurrence to solve each one of the resulting sudokus, and 
    for value in values[s]:
        new_sudoku = values.copy()
        new_sudoku[s] = value
        attempt = search(new_sudoku)
        if attempt:
            return attempt

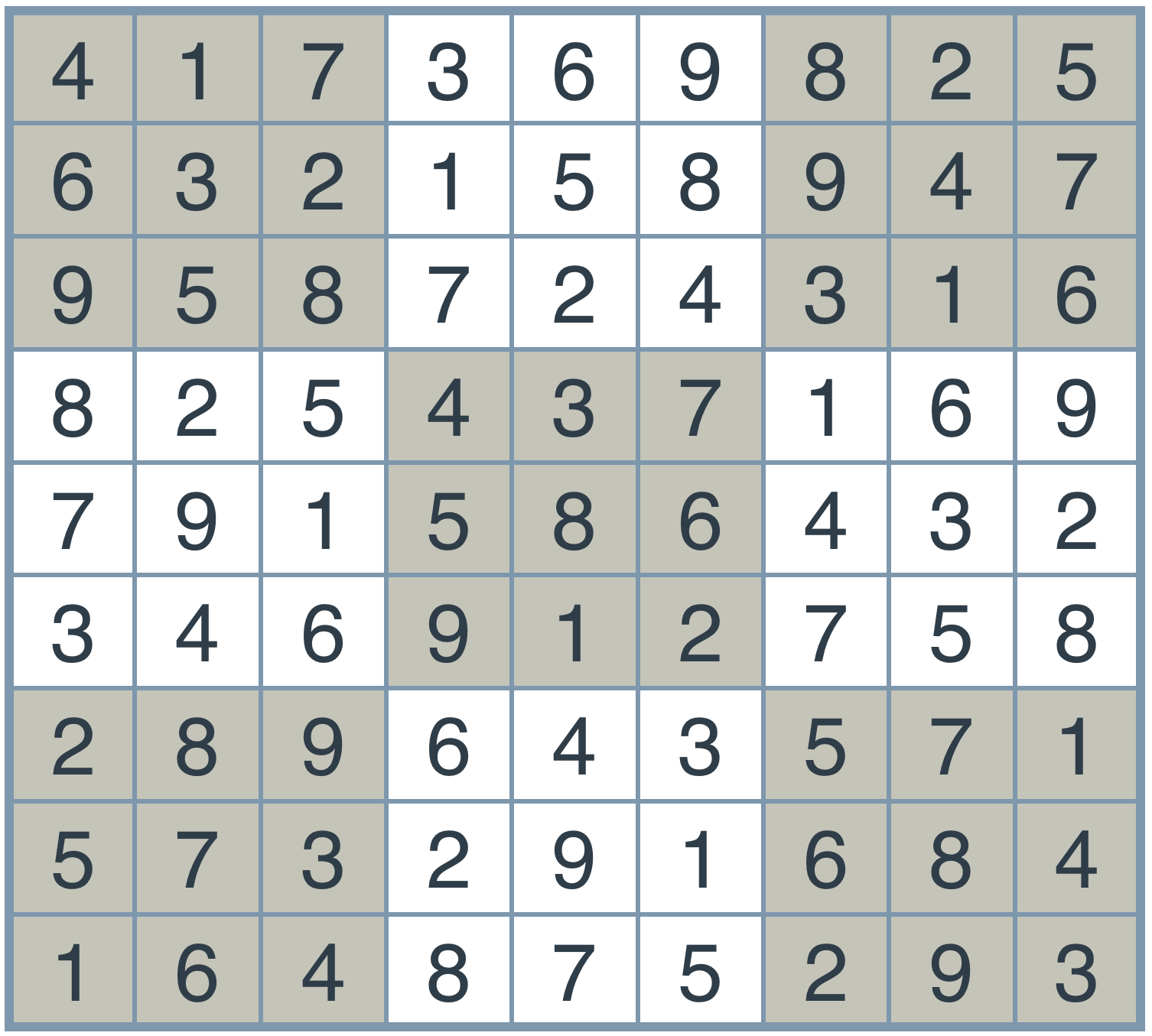
So, that seemed to do it! You should have got the following solution.